This content originally appeared on HackerNoon and was authored by Phenomenology Technology
:::info Authors:
(1) Dorian W. P. Amaral, Department of Physics and Astronomy, Rice University and These authors contributed approximately equally to this work;
(2) Mudit Jain, Department of Physics and Astronomy, Rice University, Theoretical Particle Physics and Cosmology, King’s College London and These authors contributed approximately equally to this work;
(3) Mustafa A. Amin, Department of Physics and Astronomy, Rice University;
(4) Christopher Tunnell, Department of Physics and Astronomy, Rice University.
:::
Table of Links
2 Calculating the Stochastic Wave Vector Dark Matter Signal
3 Statistical Analysis and 3.1 Signal Likelihood
4 Application to Accelerometer Studies
4.1 Recasting Generalised Limits onto B − L Dark Matter
6 Conclusions, Acknowledgments, and References
\ A Equipartition between Longitudinal and Transverse Modes
B Derivation of Marginal Likelihood with Stochastic Field Amplitude
D The Case of the Gradient of a Scalar
3.2 Projected Exclusions
To derive our limits, we construct the one-sided log-likelihood-ratio test statistic, defined as
\
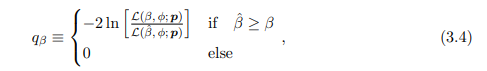
\ where βˆ is that value of β which maximises the likelihood given the observed data set p, characterising the best-fit model. This statistic is defined as a piecewise function as we only expect excess signals to be disfavoured when excluding a value of β in a one-sided test. This corresponds to values of β greater than the best-fit value. Values below this are deemed under-fluctuations and considered consistent with observation. This statistic tells us how consistent the data are with a signal defined by β compared to the best-fit model, with zero representing perfect consistency and large values indicating high inconsistency.
\

\ Ultimately, we compute 90% CL limits (αconf = 0.90) via a series of Monte Carlo (MC) simulations, following the above procedure in each MC run[8]. For a given choice of β, we
\

\

\ We show the 90% CL limit arising from our three-peak analysis in Fig. 4. Also shown are the corresponding results from two single-peak analyses focusing solely on the Compton and either one of the sum or difference peaks. These results follow the same MC procedure as above but take as the full likelihood only the Compton or the sum/difference likelihood given in Eq. (3.2). We see that the three-peak analysis produces a limit that is largely latitude-independent, rising slightly towards the pole. This is because the sensitivity axis at this latitude only has a component parallel to the Earth’s rotation axis and is thus only able to pick out the Compton peak.
\ This latitude-independent limit is in contrast with the analyses that focus on only single peaks, which are both highly sensitive to where the experiment is placed. For the study focusing on the Compton peak, the constraining power is optimal at the pole, where all of the power is contained in the Compton frequency bin, and it rapidly declines towards the equator, where the Compton peak disappears. Note that this and the three-peak results join at this point, with no difference between the approaches. Conversely, for an
\
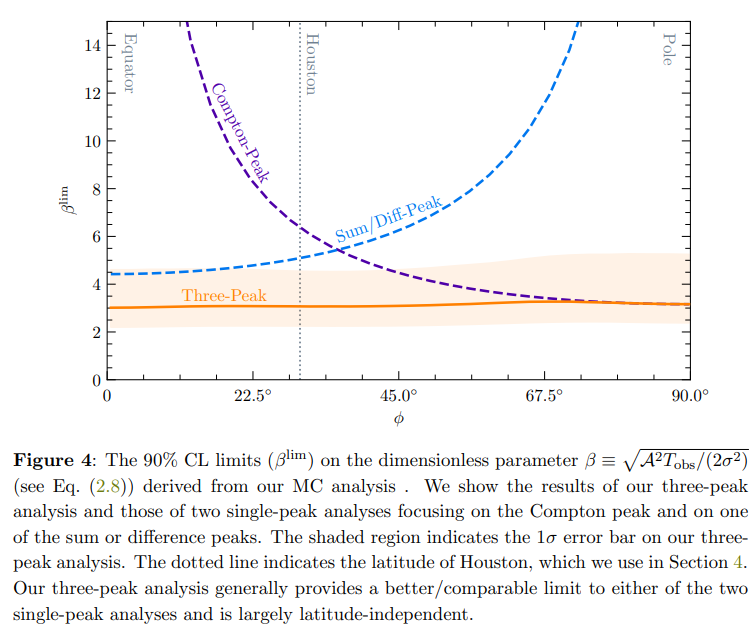
\ analysis focusing on one of the sum or difference peaks, the situation is the opposite. In this case, the results of this and the three-peak methods do not converge since half the power is contained in a single one of the sum or difference peaks at the equator; the threepeak analysis captures all of this power, whereas the single-peak analysis misses half of the power. Thus, the strength of our analysis is that the constraining power is retained no matter where an experiment is placed, such that its latitude is rendered largely irrelevant from the viewpoint of constraining a ULDM signal.
\ We emphasize that the interpretation of Fig. 4 is as a set of exclusion lines whereby background pseudodata is generated and the assumed DM signal strength is constrained. The key point is that the level of this constraint depends on the assumption one makes on the nature of the DM signal given a non-detection. Taking this signal to be only a single peak in Fourier space then leads to constraints that are generally dependent on the latitude of the experiment, rapidly weakening towards latitude extremes. On the other hand, employing the full signal model consisting of three peaks yields stronger constraints that are almost independent of the experiment placement.
\ Throughout the above analysis, we assumed that the sensitivity axis pointed in the zenith direction. However, we can relax this assumption and consider what our results would look like if this axis pointed in some different direction, say for instance directions perpendicular to the zenith—namely, the East/West and North/South directions[9]. If North/South-pointing, all of the curves in Fig. 4 would be flipped about the line ϕ = 45◦ . While the strongest limit for the Compton peak would now occur at the equator instead of the pole (and vice versa for both the sum and difference peaks), crucially we would still retain a largely latitude-independent constraint for our three-peak analysis. This is because, throughout the experiment, the directionality of the detector makes a cone, making it sensitive to the vector DM power in all the three directions. If, instead, the axis pointed towards the East/West, we would only see the sum and the difference peaks. This is because, throughout the experimental expedition, the directionality of the detector is restricted to lie on a plane (which would necessarily be perpendicular to the rotation axis of the Earth). Therefore, it is always insensitive to the power contained across the perpendicular direction, which is tied to the standalone Compton peak. One final possibility is when the directionality of the detector traces out a line throughout the experiment. This is only possible when it points parallel to the Earth’s rotation axis (at any given latitude). In this case, we would naturally be oblivious to the Earth’s rotation and hence to the sum and difference peaks, and we would only be able to resolve the Compton peak.
\ In summary, the best-case scenario is when the detector’s sensitivity axis traces out a cone. In this case, we capture all the three peaks since we are sensitive to the vector DM power across all three directions (Earth’s rotation axis and the two orthogonal directions).
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
[8] While asymptotic formulae exist for computing exclusion limits, we have opted for an MC approach to ensure proper coverage [81]. Since we are following a hybrid frequentist-Bayesian approach, we found this to be an especially pertinent check.
This content originally appeared on HackerNoon and was authored by Phenomenology Technology
Phenomenology Technology | Sciencx (2024-10-27T21:22:08+00:00) Projected Exclusions for Vector Dark Matter Detection Using Latitude-Independent Three-Peak Analysis. Retrieved from https://www.scien.cx/2024/10/27/projected-exclusions-for-vector-dark-matter-detection-using-latitude-independent-three-peak-analysis/
Please log in to upload a file.
There are no updates yet.
Click the Upload button above to add an update.
